Механика | VseFormuly | Физика

Разделы физики

Механика

Формулы движение и взаимодействие тел.

Кинематика

Скорость

При равномерном движении:

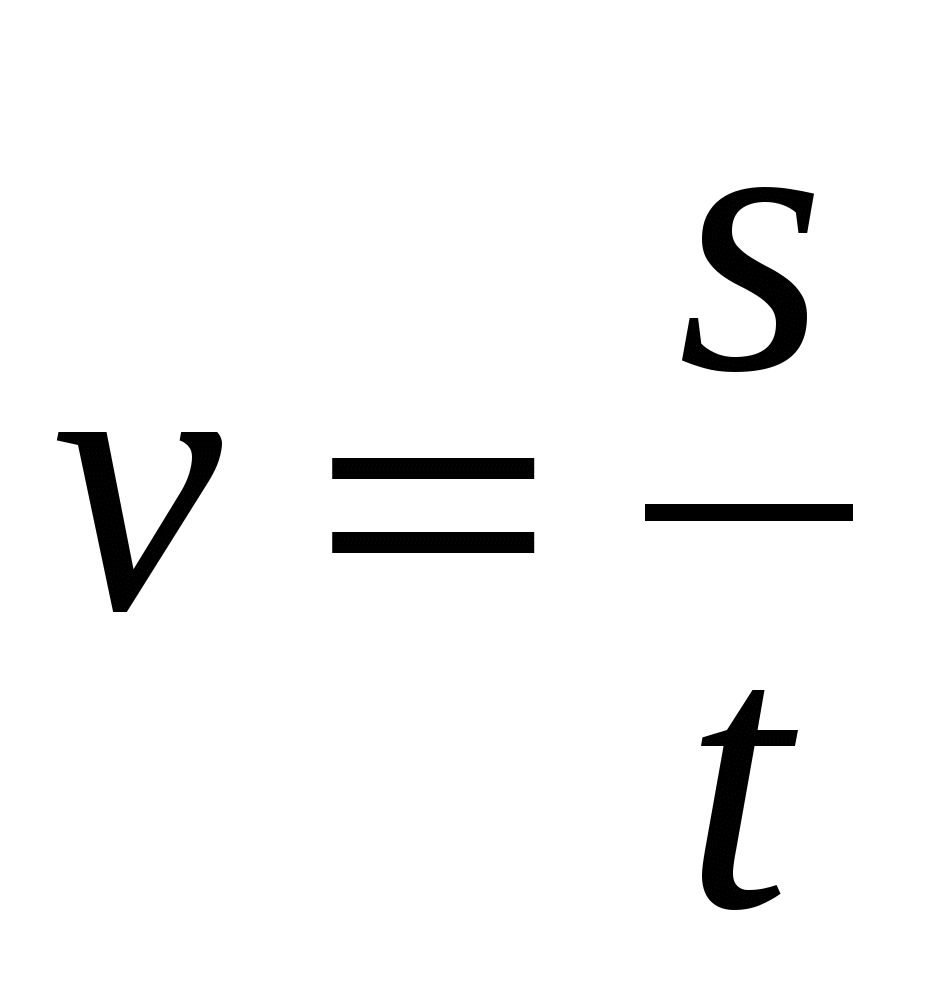
Пояснение:

υ - скорость (м/с)
S - путь (м)
t - время (с)

При равноускоренном движении:

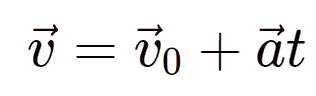
Пояснение:

υ - скорость тела (м/с)
υ0 - начальная скорость (м/с)
α - ускорение (м/с²)
t - время (с)

При свободном падении тел:

Пояснение:

υ - скорость тела (м/с)
υ0 - начальная скорость (м/с)
g - ускорение сободного падения (9,8 м/с²)

Скорость по оси X:

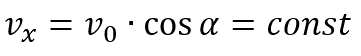
Пояснение:

υx - проекция скорости на ось X (м/с)
υ0 - начальная скорость (м/с)
cos α - косинус угла α
(между v0 и осью X)

Скорость по оси Y:

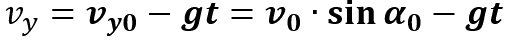
Пояснение:

υy - проекция скорости на ось Y (м/с)
υy0 - начальная скорость (м/с)
t - время
v0 - модуль начальной скорости
sin α0 - синус угла броска (α0)
g- ускорение свободного падения (9,8 м/с²)

Путь(высота)

При равномерном движении:

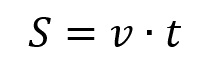
Пояснение:

S - путь (м)
υ - скорость (м/с)
t - время (с)

При равноускоренном движении:

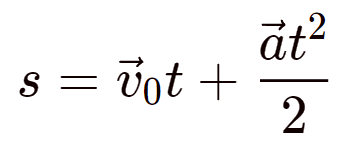
ИЛИ

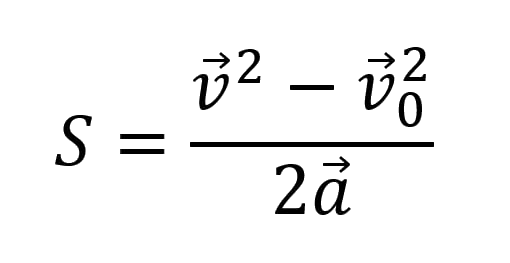
Пояснение:

S - путь (м)
υ - скорость (м/с)
υ0 - начальная скорость (м/с)
α - ускорение (м/с²)
t - время (с)

Высота подъёма:

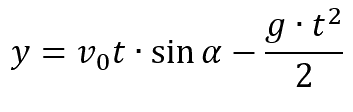
Пояснение:

y(h) - высота (м)
υ0 - начальная скорость (м/с)
t - время (с)
sin α — синус угла броска (α)
g - ускорение сободного падения (9,8 м/с²)

Максимальна высота подъёма:

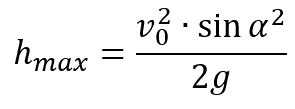
Пояснение:

hmax - максимальная высота (м)
υ0 - начальная скорость (м/с)
sin α — синус угла броска (α)
g - ускорение сободного падения (9,8 м/с²)

Высота брошенного тела:

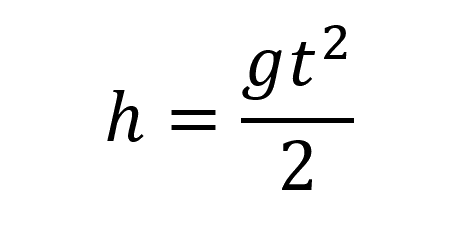
Пояснение:

h - высота (м)
t - время (c)
g - ускорение сободного падения (9,8 м/с²)

Дальность броска:

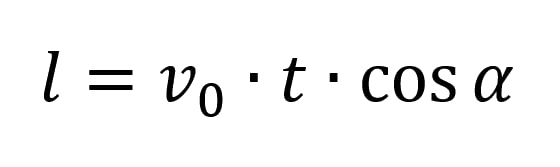
Пояснение:

l - дальность полёта
υ0 - начальная скорость (м/с)
t - время (c)
cos α - угол броска(α)

Уравнения движения

При равномерном движении:

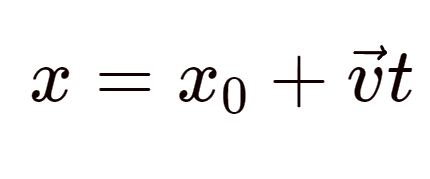
Пояснение:

x - конечная координата (м)
x0 - начальная координата (м)
υ - скорость (м/с)
t - время (с)

При равноускоренном движении:

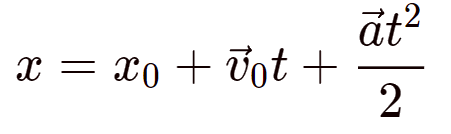
Пояснение:

x - конечная координата (м)
x0 - начальная координата (м)
υ0 - начальная скорость (м/с)
t - время (с)
α - ускорение (м/с²)

Тело брошенное по углом, по оси X:

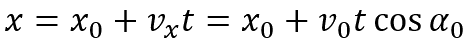
Пояснение:

x - конечная координата (м)
x0 - начальная координата (м)
υx - проекция скорости (м/с)
t - время (с)
υ0 - начальная скорость (м/с)
cos α0 - косинус угла броска α0

Тело брошенное по углом, по оси Y:

Пояснение:

y - конечная координата (м)
y0 - начальная координата (м)
υ0 - начальная скорость (м/с)
t - время (с)
sin α0 — синус угла броска (α0)
g - ускорение сободного падения (9,8 м/с²)

Ускорение

При равномерном движении:

α = 0

При равноускоренном движении:

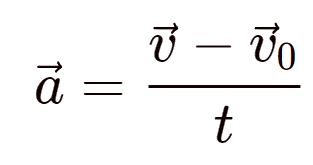
Пояснение:

α - ускорение (м/с²)
υ - скорость тела (м/с)
υ0 - начальная скорость (м/с)
t - время (с)

При свободном падении:

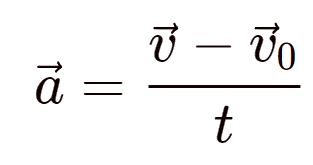
Пояснение:

α(g) - ускорение (м/с²)
υ - скорость тела (м/с)
υ0 - начальная скорость (м/с)
t - время (с)

Движение по окружности

Период:

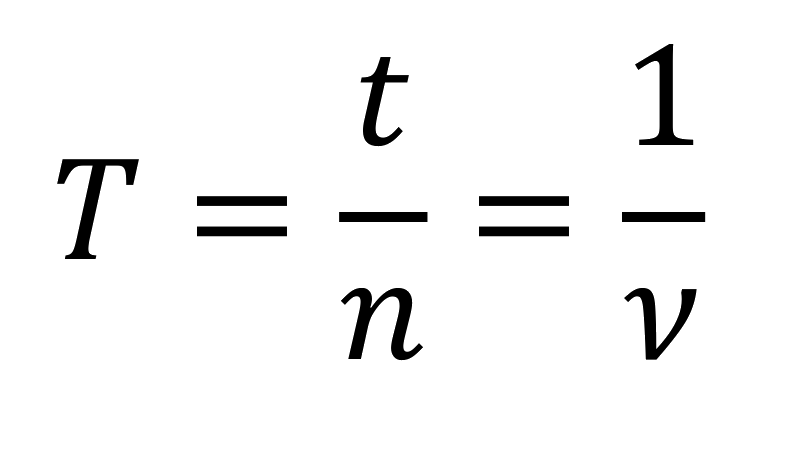
Пояснение:

T - период (с)
t - время (с)
n - число обротов
ν(ню) – частота (Гц)

Частота:

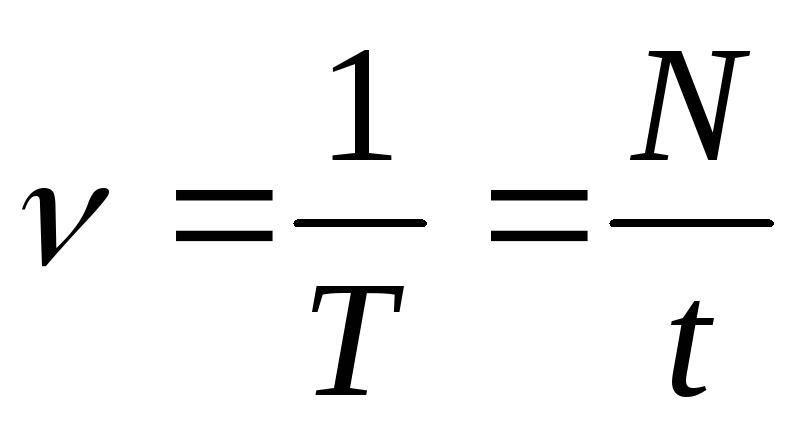
Пояснение:

ν(ню) – частота (Гц)
T - период (с)
t - время (с)
N(n) - число обротов

Линейная скорость движения материальной точки по окружности:

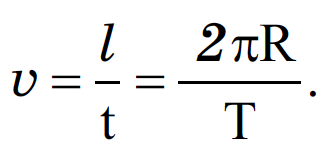
Пояснение:

υ - линейная скорость (м/с)
l - длинна окружности (м)
t - время (с)
R - радиус окружности (м)
T - период (с)
π = 3,14

Угловая скорость:

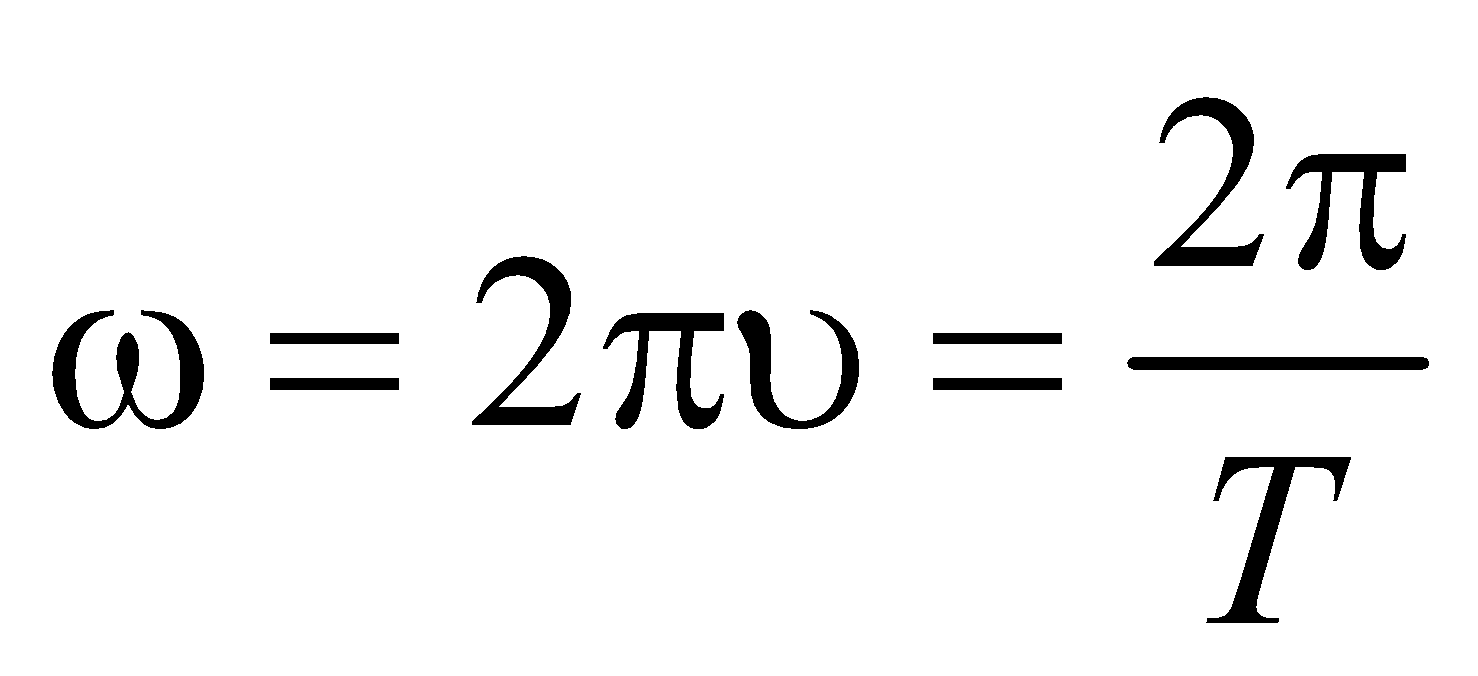
Пояснение:

ω(омега) - угловая скорость(рад/с)
ν(ню) – частота (Гц)
T - период (с)
π = 3,14

Зависимость угловой скорости от линейной:

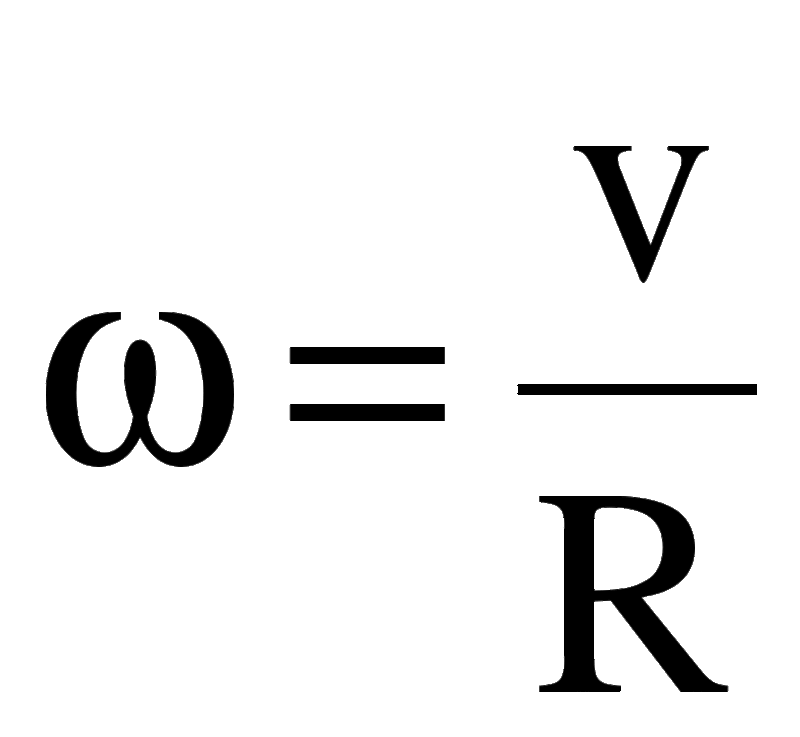
Пояснение:

ω(омега) - угловая скорость(рад/с)
υ - линейная скорость (м/с)
R - радиус окружности (м)

Центростремительное ускорение:

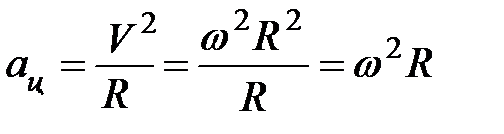
Пояснение:

αцc - центростремительное ускорение (м/с²)
υ - линейная скорость (м/с)
R - радиус окружности (м)
ω(омега) - угловая скорость(рад/с)

Динамика

Законы Ньютона

Первый закон Ньютона:

Тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или действие этих сил скомпенсировано.

Пояснение:

F1 + F2 + F3 + ... Fn = 0

Второй закон Ньютона:

Ускорение тела в инерциальной системе отсчёта прямо пропорционально приложенной к нему силе и обратно пропорционально массе.

Пояснение:

F - равнодействующая сил (н)
m - масса тела (кг)
a - ускорение (м/с²)

Третий закон Ньютона:

Силы взаимодействия двух материальных точек равны по величине, противоположно направлены, и действуют вдоль прямой, соединяющей эти точки.

Пояснение:

F1 – сила действующая со стороны первого тела (Н)
F2 – сила действующая со стороны второго тела (Н)

Космические скорости

Первая космическая скорость:

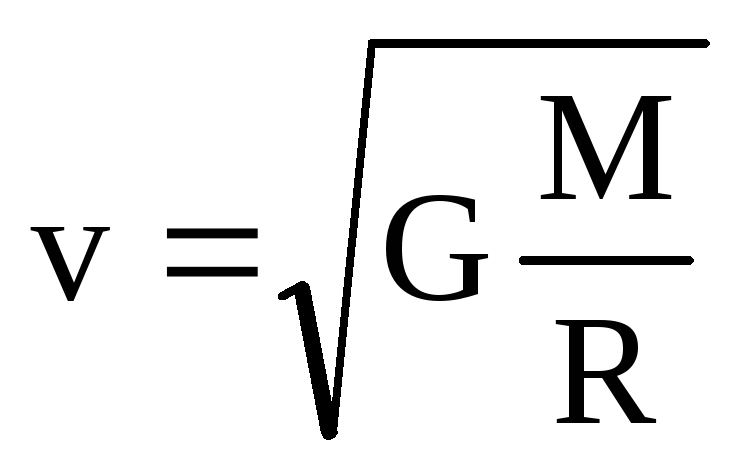
Пояснение:

- минимальная скорость, необходимая, чтобы тело стало искусственным спутником планеты и двигалось по круговой орбите у её поверхности (без учёта атмосферы).
υ1 - первая космическая (м/с)
G - гравитационная постоянная (≈6,67430 x 10-11 (м3•кг-1/c-2))
M - масса планеты (кг)
(для Земли ≈ 5,972 x 1024 (кг))
R - радиус планеты (м)
(для Земли ≈ 6,371 x 106 (м))
Для Земли: v1 ≈ 7,91 км/с.

Вторая космическая скорость:

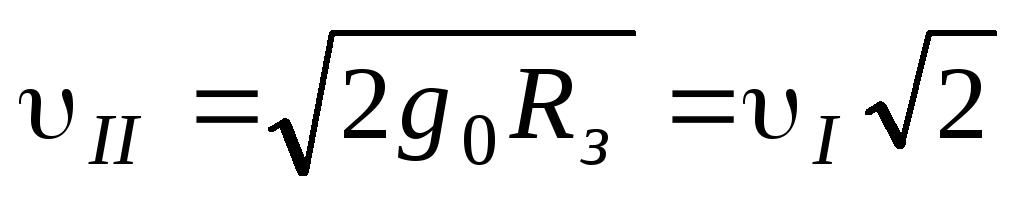
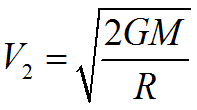
Пояснение:

- минимальная скорость, позволяющая телу полностью преодолеть гравитацию планеты и уйти в космическое пространство по параболической траектории (без дальнейшего разгона).
υ1 - первая космическая (м/с)
υ2 - вторая космическая (м/с)
g - ускорение свободного падения (9,8 м/с²)
G - гравитационная постоянная (≈6,67430 x 10-11 (м3•кг-1/c-2))
M - масса планеты (кг)
(для Земли ≈ 5,972 x 1024 (кг))
R(Rз) - радиус планеты (м)
(для Земли ≈ 6,371 x 106 (м))
Для Земли: v2 ≈ 11,2 км/с.

Третья космическая скорость:

Пояснение:

- минимальная скорость, необходимая, чтобы тело, стартуя с Земли, покинуло Солнечную систему (преодолело притяжение и Солнца, и Земли).
Для Земли: v3 ≈ 16,65 км/с (значение зависит от направления запуска относительно орбитального движения Земли).

Четвертая космическая скорость:

υ4 = √2 x υгал

Пояснение:

- минимальная скорость, чтобы покинуть галактику (преодолеть гравитацию Млечного Пути в окрестности Солнца).
υ4 - четвертая космическая(м/с)
υгал - вторая космическая (м/с)
υгал - характерная скорость вращения звёзд в галактике вокруг её центра (м/с)
(в окрестности Солнца ≈ 220 км/с)
Для окрестности солнца:
v4 ≈ 550 км/с.
(очень приблизительная оценка, так как распределение массы в галактике неоднородно)

Природные силы

Сила всемирного тяготения:

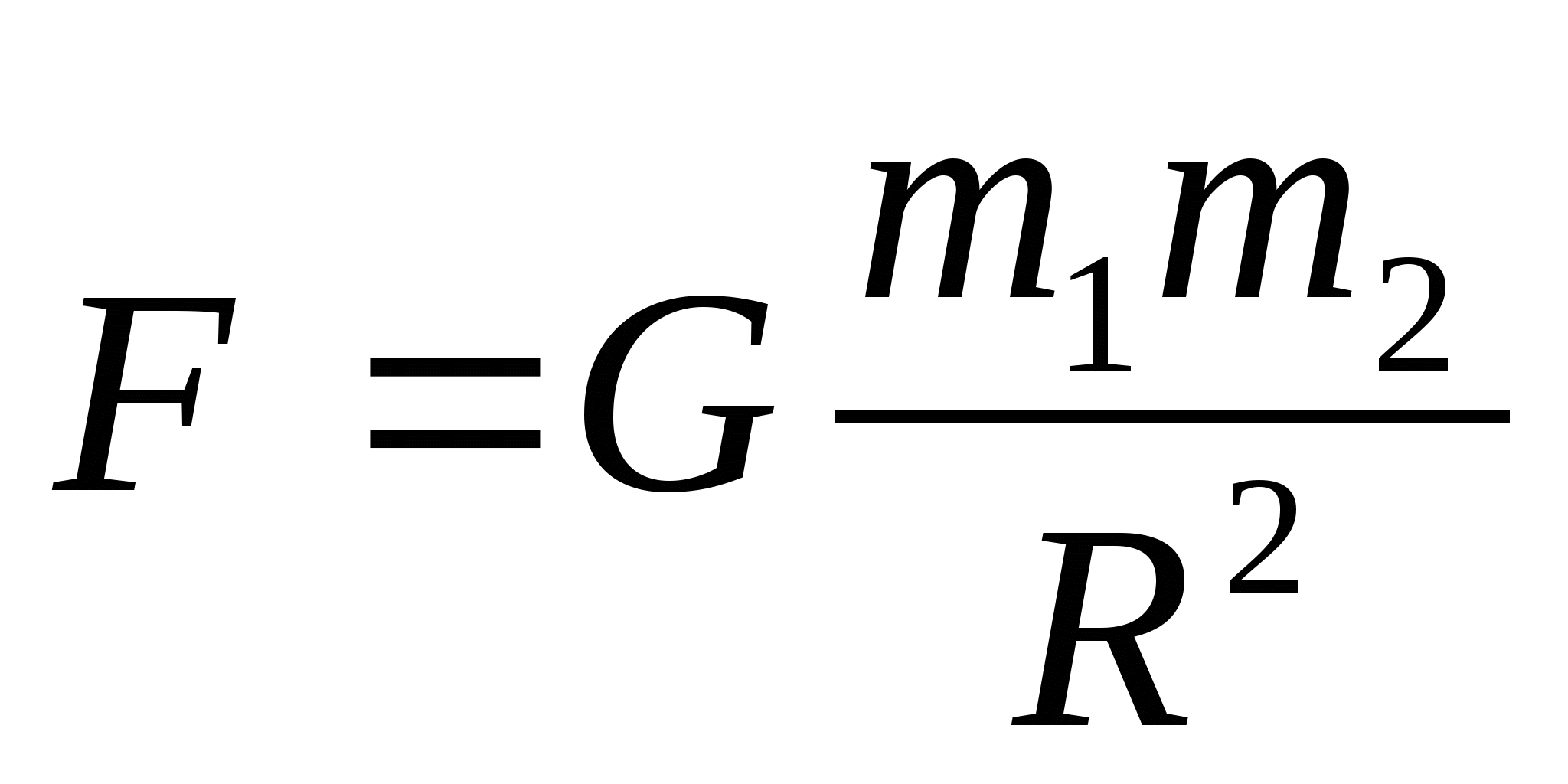
Пояснение:

F - Сила тяготения (н)
G - гравитационная постоянная (≈6,67430 x 10-11 (м3•кг-1/c-2))
m1 - масса первого тела (кг)
m2 - масса первого тела (кг)
R - расстояние между центрами масс этих тел (м)

Сила тяжести:

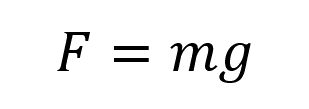
Пояснение:

F - Сила тяжести (н)
m - масса тела (кг)
g - ускорение свободного падения (9,8 м/с²)

Сила упругости (закон Гука):

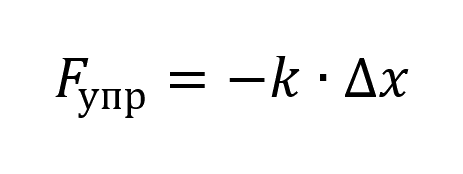
Пояснение:

Fупр - Сила упругости (н)
k - жёсткость (н/м)
Δx - абсолютное удлинение (м)
Δx = Δl = l - l0

Δl - изменение длины (м)
l - конечная длинна (м)
l0 - начальная длинна (м)

Cила трения:

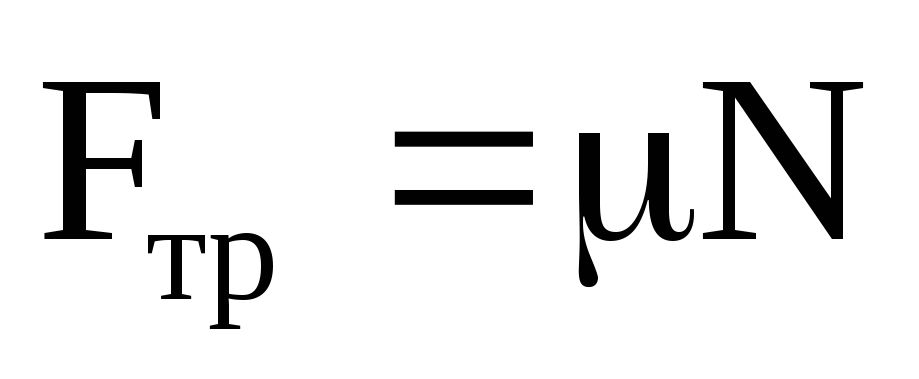
Пояснение:

Fтр - Сила трения (н)
μ(мю) - коэффициент трения
N - сила нормальной реакции опоры (н)
(значения μ в таблице)

Cила трения покоя:

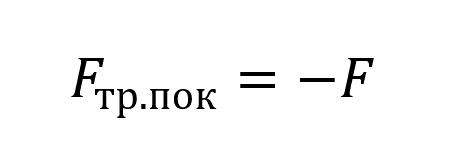
Пояснение:

Fтр.пок - Сила трения покоя (н)
-F - толкающая сила (н)

Cила трения скольжения:

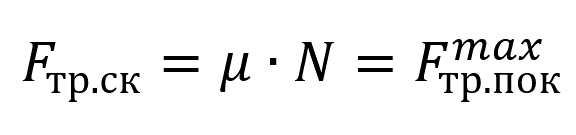
Пояснение:

Fтр.ск - сила трения скольжения (н)
μ(мю) - коэффициент трения
N - сила нормальной реакции опоры (н)
F
max тр.пок
- максимальная сила трения покоя (н)
(значения μ в таблице)

Cила реакции опоры:

N = F = mg

Пояснение:

F - сила (н)
m - масса (кг)
g - ускорение свободного падения (9,8 м/с²)

Вес тела – сила, с которой тело давит на опору или подвес.

Вес тела в состоянии покоя:

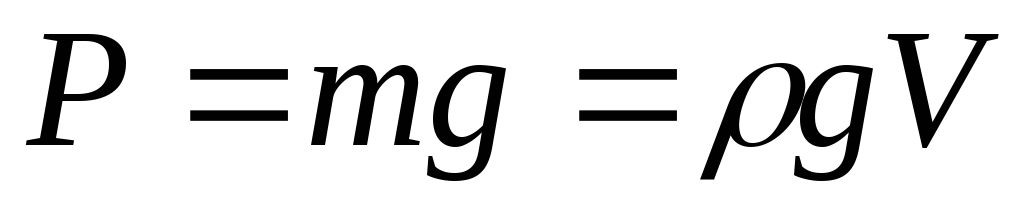
Пояснение:

P - вес тела (н)
m - масса тела (кг)
ρ(ро) - плотность тела (кг/м³)
v - объём тела (м³)
g - ускорение свободного падения (9,8 м/с²)

Вес тела, движущегося с ускорением вверх:

P = m(g + a)

Пояснение:

P - вес тела (н)
m - масса тела (кг)
a - ускорение (м/с²)
g - ускорение свободного падения (9,8 м/с²)

Вес тела, движущегося с ускорением вниз:

P = m(g - a)

Пояснение:

P - вес тела (н)
m - масса тела (кг)
a - ускорение (м/с²)
g - ускорение свободного падения (9,8 м/с²)

Вес тела при свободном падении:

P = 0

Натяжение нити

При вертикальном подвесе груза:

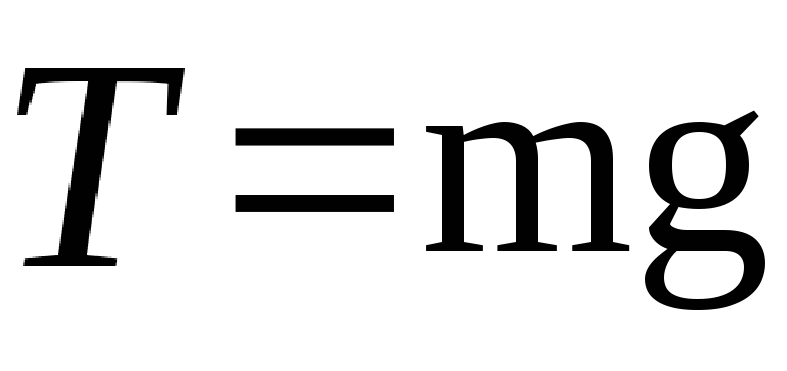
Пояснение:

T - натяжение нити (н)
m - масса груза (кг)
g - ускорение свободного падения (9,8 м/с²)

Если система движется с ускорением вверх:

T = m(g + a)

Пояснение:

Т - натяжение нити (н)
m - масса груза (кг)
a - ускорение (м/с²)
g - ускорение свободного падения (9,8 м/с²)

Если система движется с ускорением вниз:

T = m(g - a)

Пояснение:

Т - натяжение нити (н)
m - масса груза (кг)
a - ускорение (м/с²)
g - ускорение свободного падения (9,8 м/с²)

Подвешенный груз действует на нить под углом :

T = mg × cos α

Пояснение:

T - натяжение нити (н)
m - масса груза (кг)
cos α - угол отклонения
g - ускорение свободного падения (9,8 м/с²)

Если действует сила Архимеда:

T = mg - FA

Пояснение:

Т - натяжение нити (н)
m - масса груза (кг)
FA - сила Архимеда (н)
g - ускорение свободного падения (9,8 м/с²)

Статика

Условия равновесия

Первое условие:

Сумма всех внешних сил, действующих на тело, должна быть равна нулю.

Пояснение:

F1 + F2 + F3 + ... Fn = 0

Второе условие:

Второе условие равновесия твёрдого тела записывается как алгебраическая сумма всех моментов сил, действующих на тело, равна нулю.

Пояснение:

M1 + M2 + M3 + ... Mn = 0

Условие равновесия рычага:

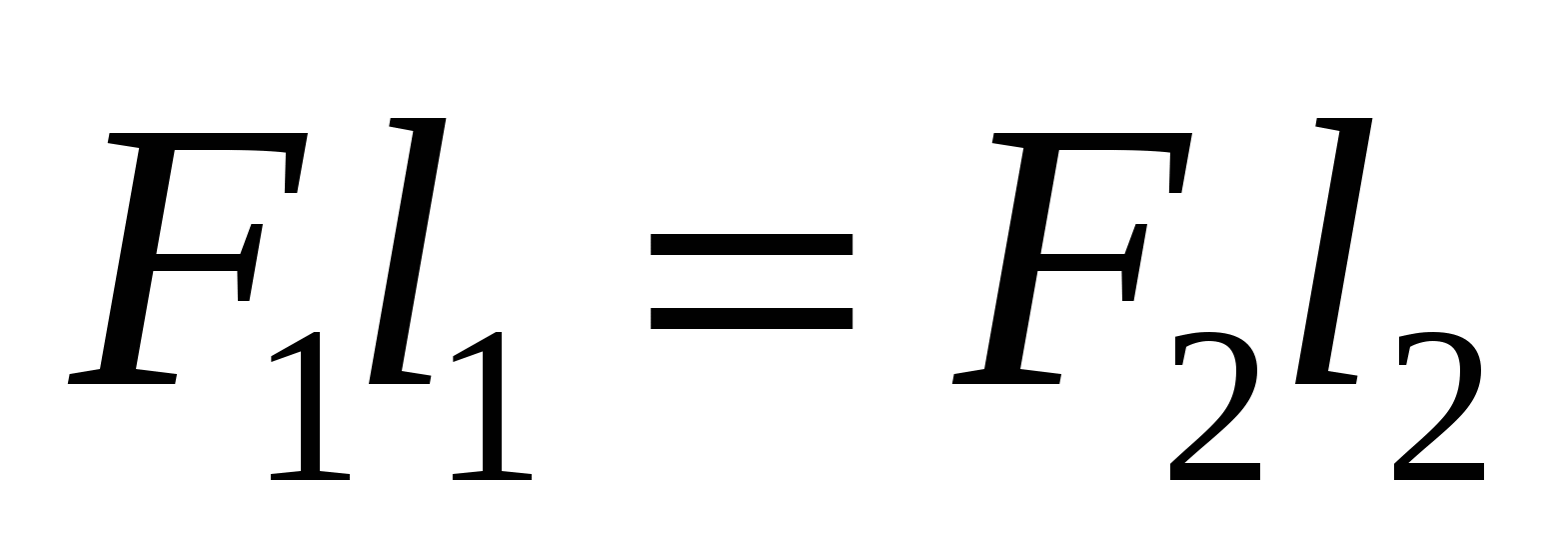
Пояснение:

F1,2 - силы (н)
l1,2 - плечи сил (м)

Момент силы:

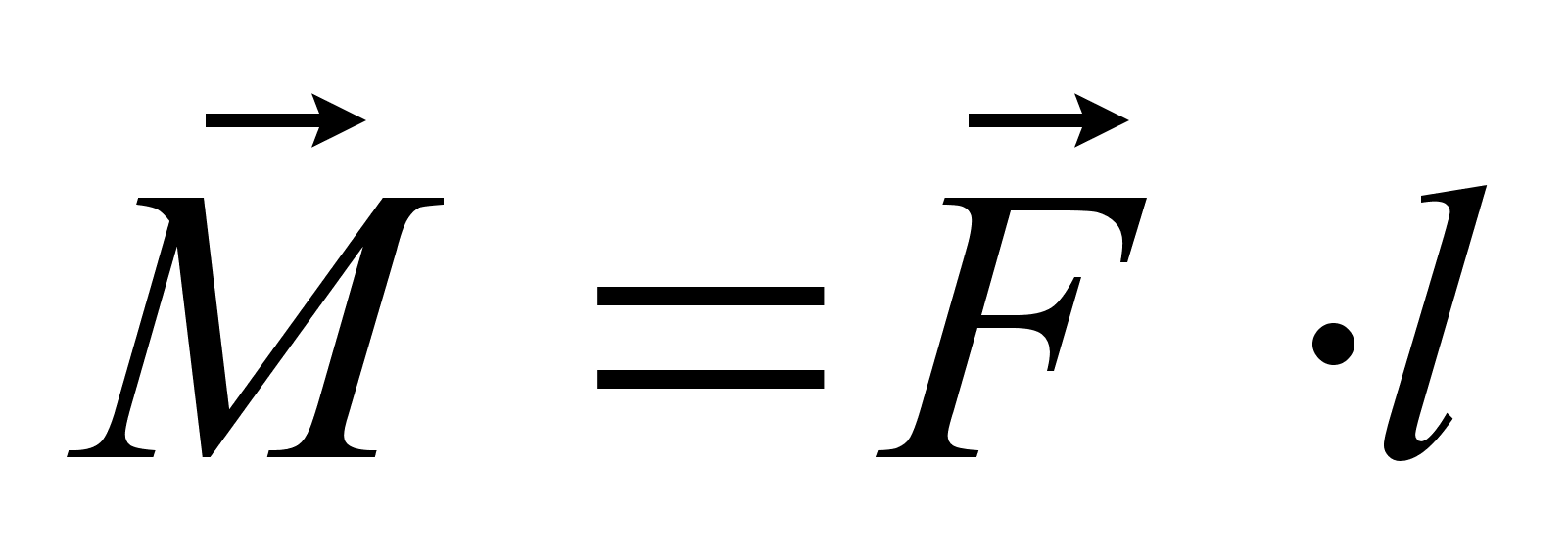
Пояснение:

M - момент силы (Н•м)
F - сила (н)
l - плечо силы (м)

Момент инерции материальной точки:

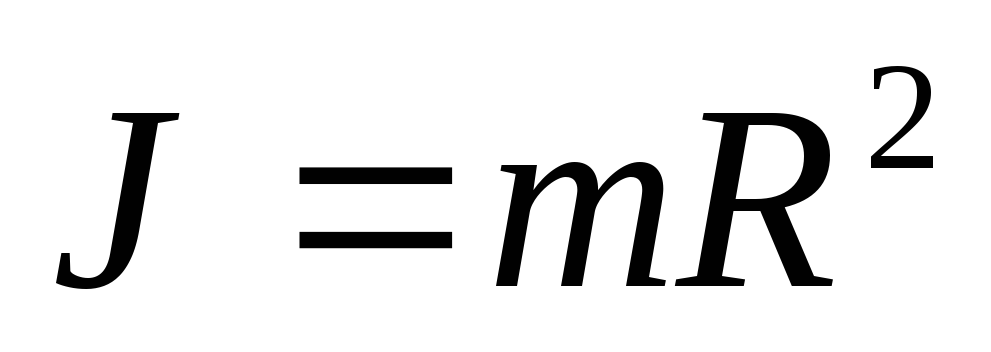
Пояснение:

J - момент инерции (кг · м²)
m - масса точки (кг)
r - расстояние до оси вращения (м)

Законы сохранения

Механическая энергия

Полная механическая энергия:

Емех=Ек+Еп

Пояснение:

Eк - кинетическая энергия (Дж)
Eп - потенциальная энергия (Дж)

Закон сохранения энергии:

Ек1+Еп1=Ек2+Еп2

Пояснение:

Eк - кинетическая энергия (Дж)
Eп - потенциальная энергия (Дж)

Потенциальная энергия в поле гравитации:

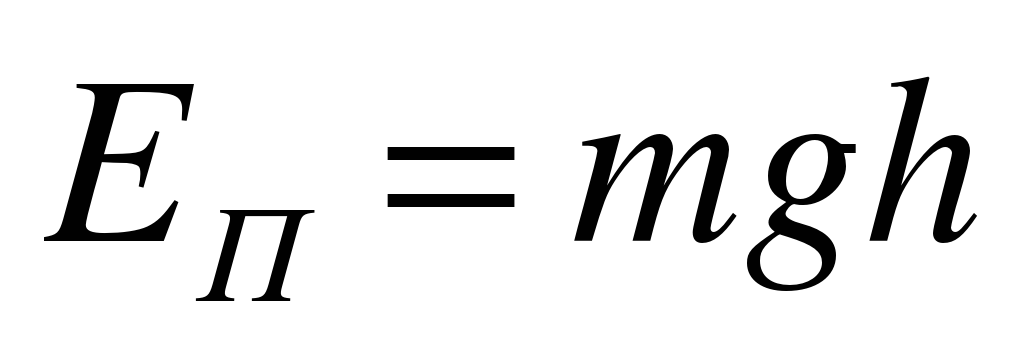
Пояснение:

Eп - потенциальная энергия (Дж)
m - масса тела (кг)
h - высота (м)
g - ускорение свободного падения (м/с²)

Потенциальная энергия у пружины:

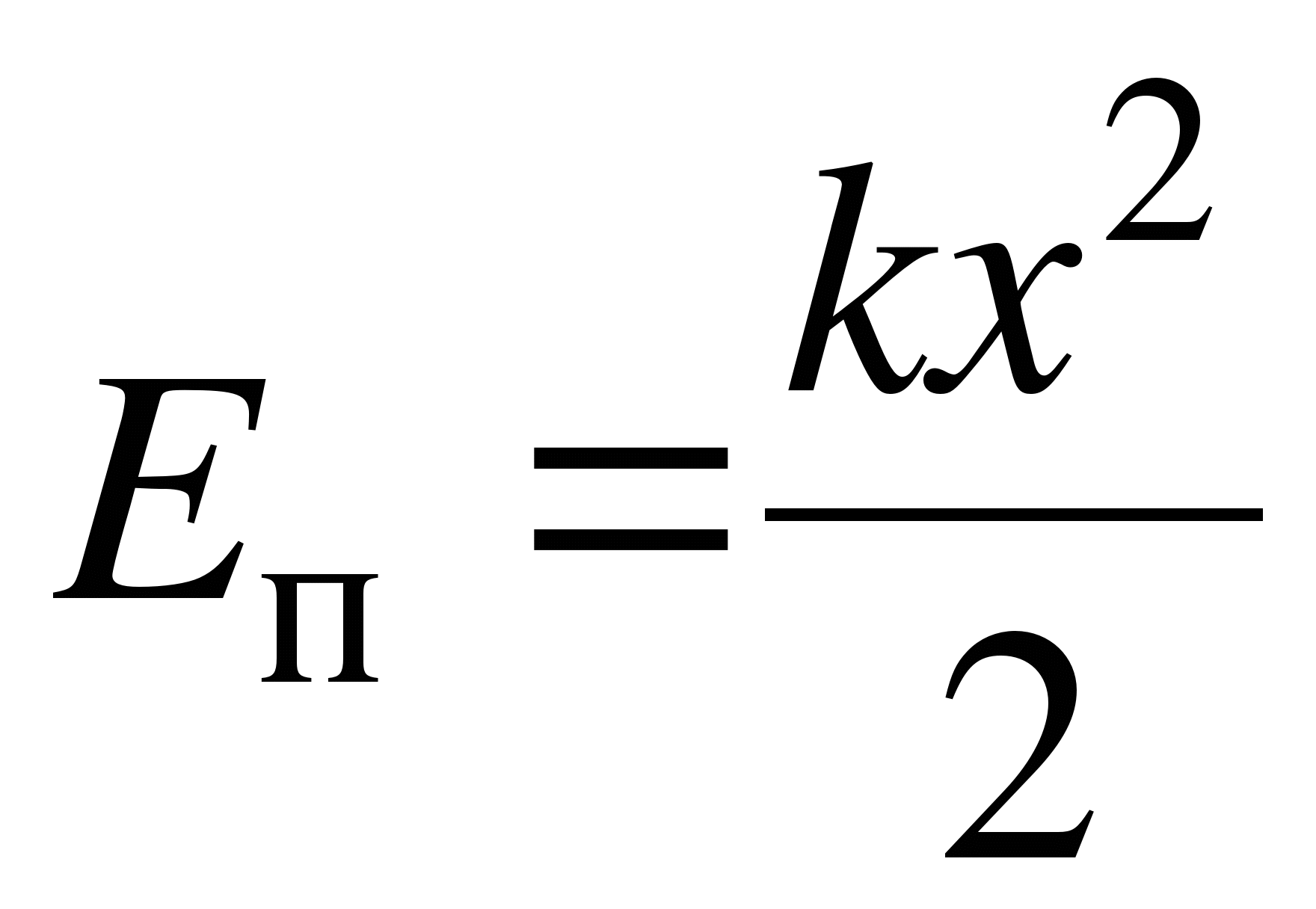
Пояснение:

Eп - потенциальная энергия (Дж)
k - жёсткость (н/м)
x - удлинение (м)

Кинетическая энергия:

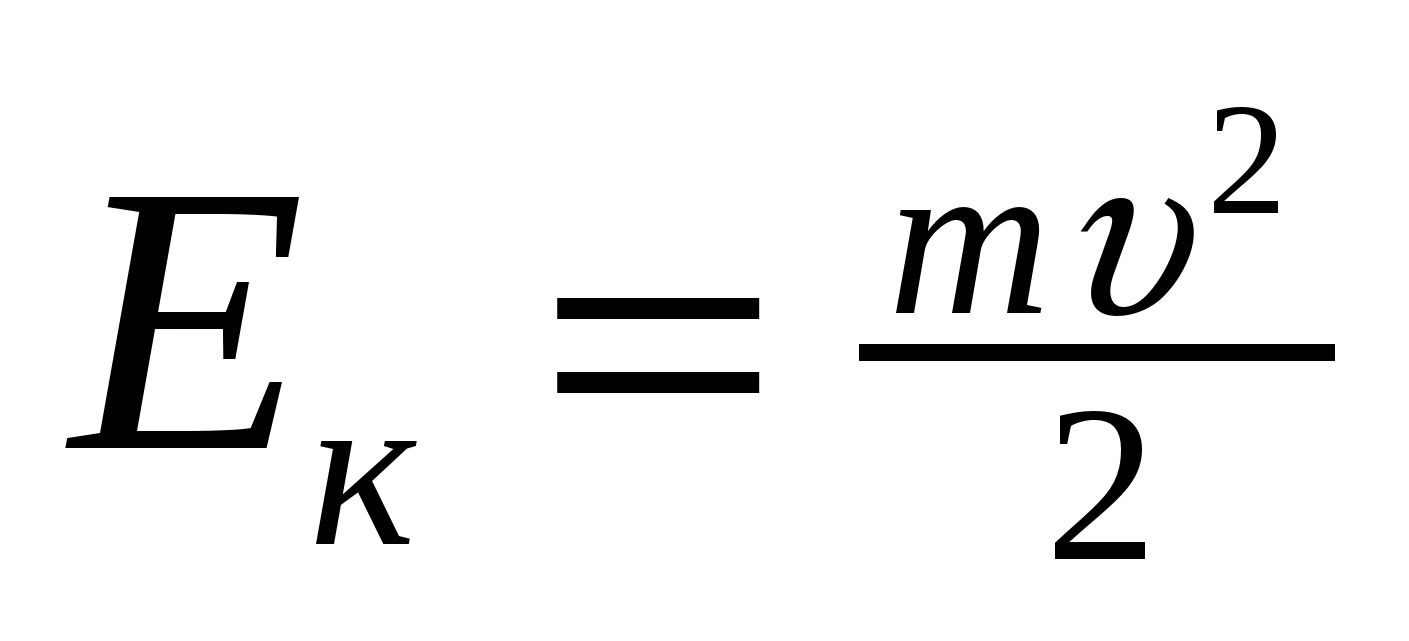
Пояснение:

Eк - кинетическая энергия (Дж)
m - масса тела (кг)
υ - скорость тела (м/с)

Работа потенциальной энергии:

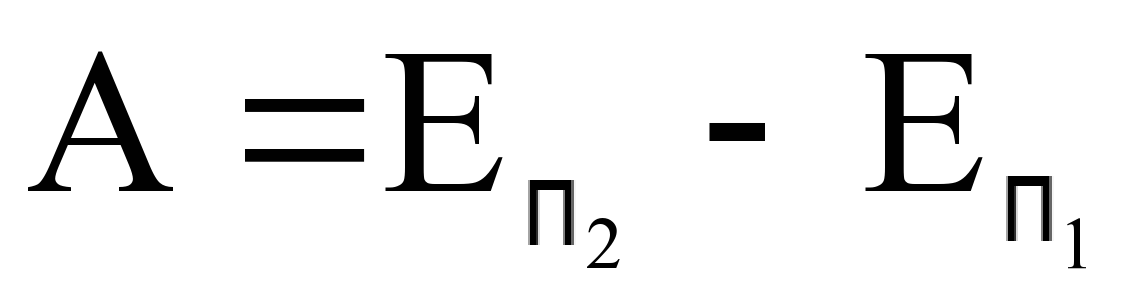
Пояснение:

А - работа (Дж)
Eп1 - потенциальная энергия в начальном состоянии (Дж)
Eп2 - потенциальная энергия в конечном состоянии (Дж)

Работа кинетической энергии:

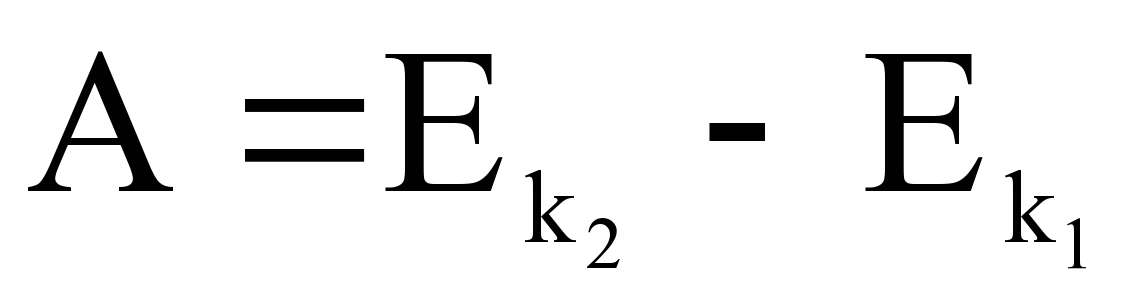
Пояснение:

А - работа (Дж)
Eк1 - кинетическая энергия в начальном состоянии (Дж)
Eк2 - кинетическая энергия в конечном состоянии (Дж)

Импульс тела

Импульс тела:

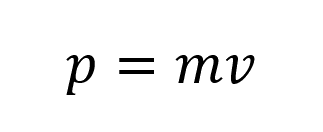
Пояснение:

P - импульс (кг • м/с)
m - масса тела (кг)
υ - скорость тела (м/с)

Импульс силы:

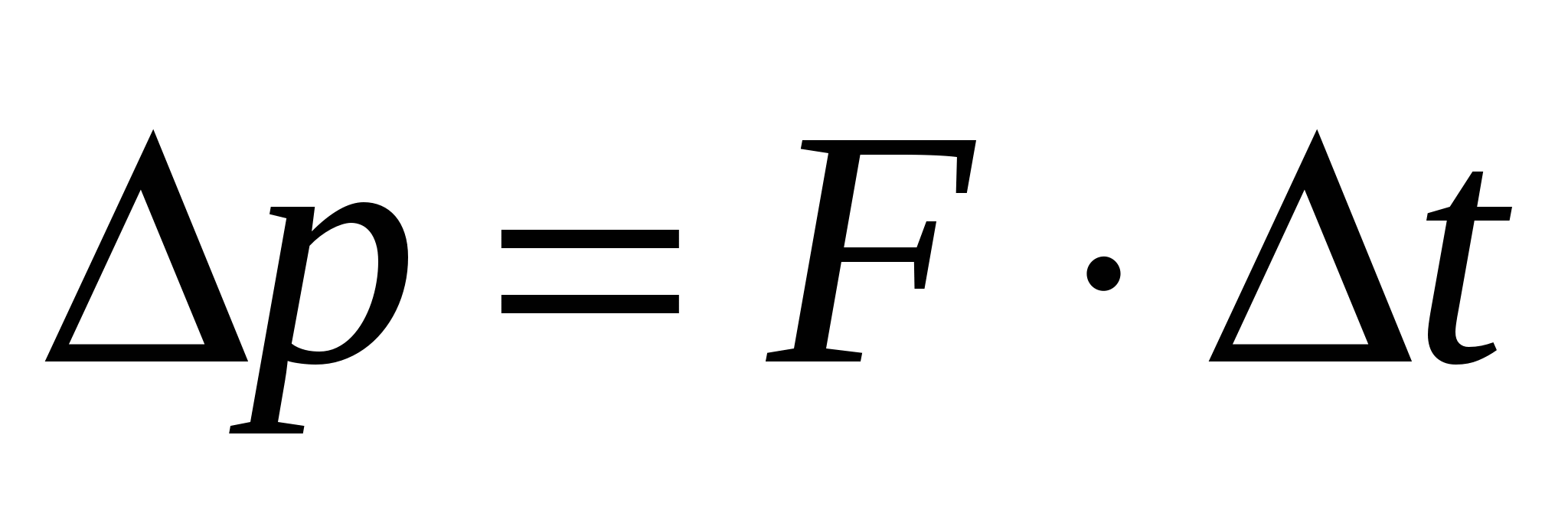
Пояснение:

ΔP - изменение импульса (кг • м/с)
F - сила (н)
Δt - время (с)

Закон сохранения импульса:

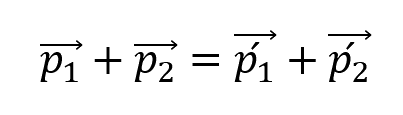
Пояснение:

p1, p2 - импульс тел до взаимодействия (кг • м/с)
p1`, p2` - импульс тел после взаимодействия (кг • м/с)

Момент импульса:

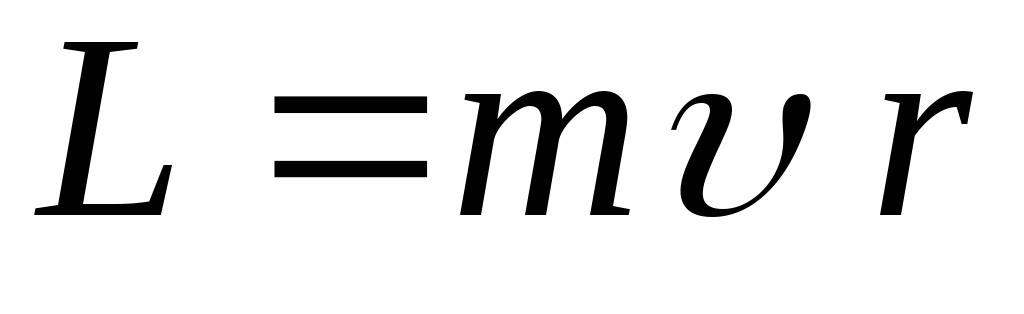
Пояснение:

L - момент импульса (кг · м²/с)
m - масса материальной точки (кг)
v - линейная скорость точки (м/с)
r - радиус окружности (м)

Механическая работа

Механическая работа трения:

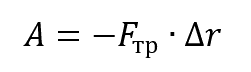
Пояснение:

А - работа трения (Дж)
Fтр - сила трения (н)
Δr - перемещение тела (м)

Мех.работа, при α = 0°:

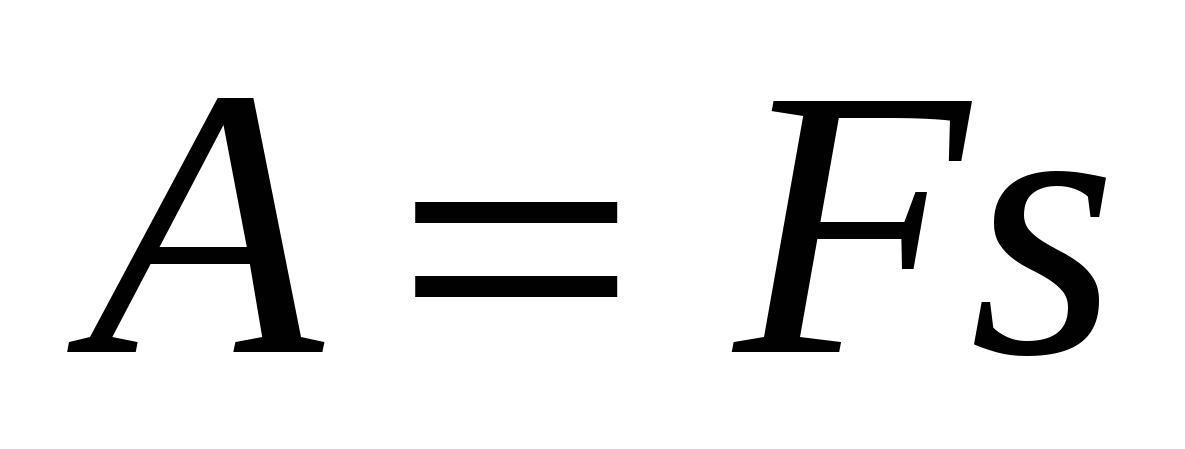
Пояснение:

А - работа (Дж)
F - сила (н)
S - перемещение (м)
α - угол между F и S

Мех.работа, при 0° < α < 90°:

Пояснение:

А - работа (Дж)
F - сила (н)
S - перемещение (м)
α - угол между F и S

Мех.работа, при α = 90°:

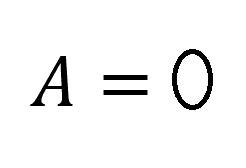
Пояснение:

А - работа (Дж)
α - угол между F и S

Мех.работа, при 90° < α < 180°:

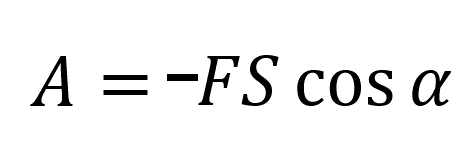
Пояснение:

А - работа (Дж)
F - сила (н)
S - перемещение (м)
α - угол между F и S

Мех.работа, при α = 180°:

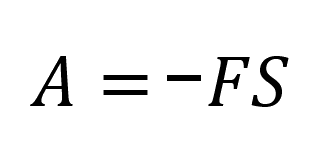
Пояснение:

А - работа (Дж)
F - сила (н)
S - перемещение (м)
α - угол между F и S
ек

Мощность:

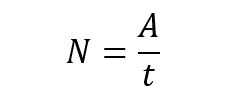
Пояснение:

N - мощность (Вт)
А - работа (Дж)
t - время (с)

Мощность мгновения:

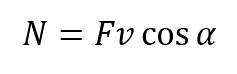
Пояснение:

N - мощность (Вт)
F - сила (н)
υ - скорость (м/с)
α - угол между F и υ

Механические колебания и волны

Характеристики механических колебаний

Период:

Пояснение:

T - период (с)
t - время (с)
n - число обротов
ν(ню) – частота (Гц)

Частота:

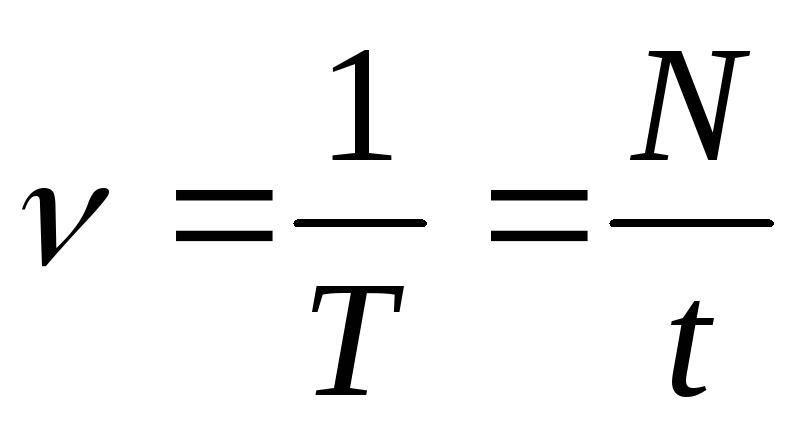
Пояснение:

ν(ню) – частота (Гц)
T - период (с)
t - время (с)
N(n) - число обротов

Циклическая частота:

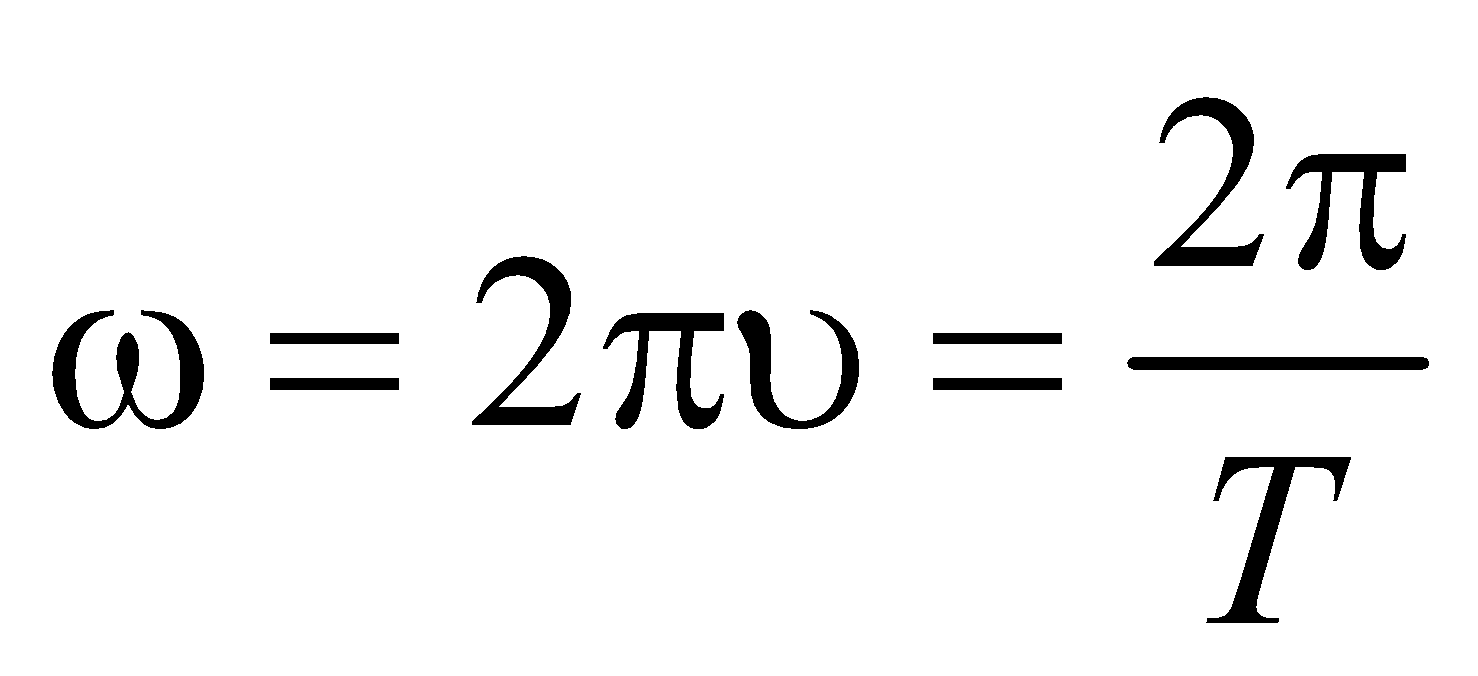
Пояснение:

ω(омега) - циклическая частота (рад/с)
ν(ню) – частота (Гц)
T - период (с)
π = 3,14

Маятники

Период математического маятника:

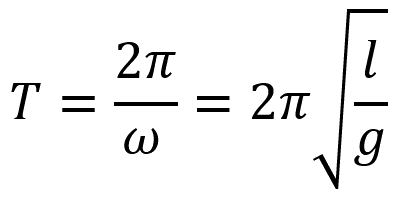
Пояснение:

T - период (с)
π = 3,14
ω - циклическая частота (рад/с)
l - длинна нити (м)
g - ускорение свободного падения (9,8 м/с²)

Период пружинного маятника:

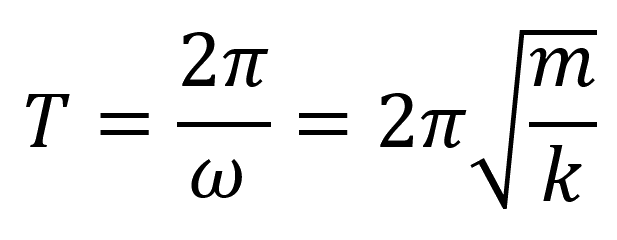
Пояснение:

T - период (с)
π = 3,14
ω - циклическая частота (рад/с)
m - масса груза (кг)
k - жесткость пружины (н/м)

Полная механическая энегрия маятника

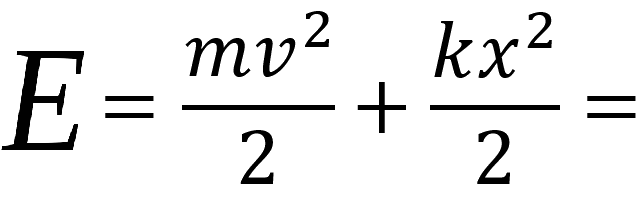
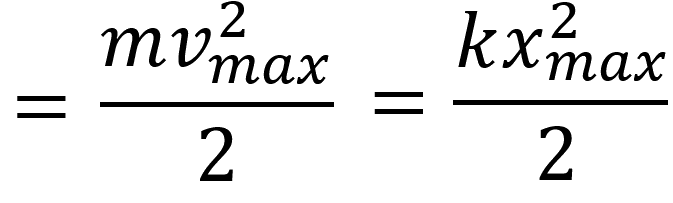
Пояснение:

E - механическая энегрия маятника (Дж)
m - масса тела (кг)
υ - скорость тела (м/с)
k - жёсткость пружины (н/м)
x - удлинение пружины (м)
υmax - скорость тела(амплитуда) (м/с)
xmax - удлинение пружины(амплитуда) (м)

Резонанс:

Условие резонанса:

νсоб = νвын

νсоб – собственная частота системы (Гц)
νвын – частота вынужденных колебаний (Гц)

Пояснение:

- это резкое возрастание амплитуды вынужденных колебаний системы при совпадении частоты вынуждающей силы с собственной частотой колебаний системы.

Гармонические колебания(координата тела):

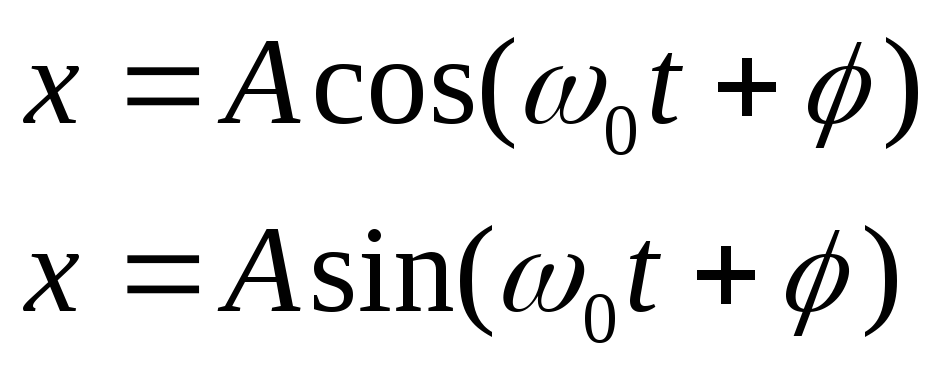
Пояснение:

x - координата тела (м)
A - амплитуда колебаний
ω0 - циклическая частота (рад/с)
t - время (с)
φ (фи) — начальная фаза (рад)
(ωt + φ) - фаза колебания (рад)

Гармонические колебания(координата скорости)

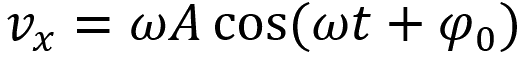
Пояснение:

υx - координата скорости (м/с)
A - амплитуда колебаний
ω - циклическая частота (рад/с)
ωA = υmax
t - время (с)
φ0(фи) - начальная фаза (рад)
(ωt + φ) - фаза колебания (рад)

Гармонические колебания(координата ускорения)

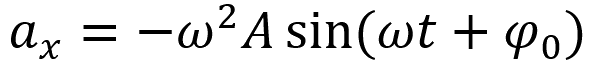
Пояснение:

αx - координата ускорения (м/с)
A - амплитуда колебаний
ω - циклическая частота (рад/с)
ω2A = αmax
t - время (с)
φ0(фи) - начальная фаза (рад)
(ωt + φ) - фаза колебания (рад)

Механические волны

Скорость волны:

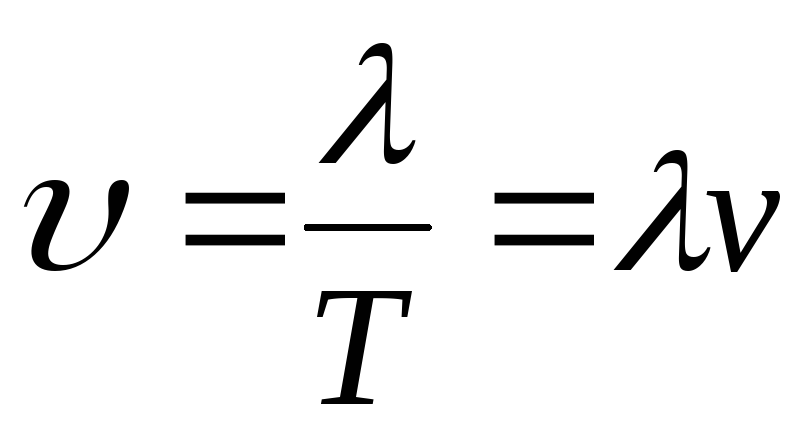
Пояснение:

υ - скорость волны (м/с)
λ - длинна волны (м)
T - период (с)
ν – частота (Гц)

Гидростатика и аэростатика

Давление жидкостей и газов

Закон Паскаля для жидкостей:

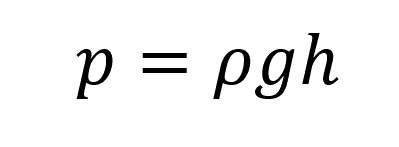
Пояснение:

- гидростатическое давление, которое оказывает столб жидкости на дно и стенки сосуда.
p - давление (Па)
ρ(ро) - плотность жидкости (кг/м³)
h - высота столба жидкости (м)
g - ускорение свободного падения (9,8 м/с²)
(значения ρв таблице)

Закон Паскаля для газов:

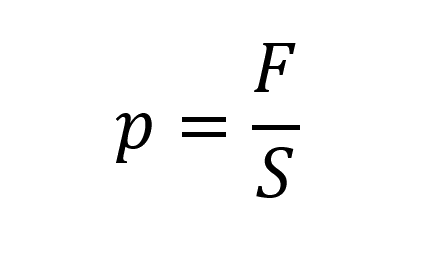
Пояснение:

- гидростатическое давление, которое оказывает столб жидкости на дно и стенки сосуда.
p - давление (Па)
F - приложенная сила (н)
S - площадь поверхности/сосуда (м²)

Полное давление в любой точке жидкости:

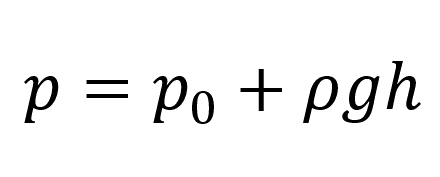
Пояснение:

p - давление жидкости (Па)
p0 - давление на её свободной поверхности (Па)
ρ(ро) - плотность жидкости (кг/м³)
g - ускорение свободного падения (9,8 м/с²)
h - высота столба жидкости (м)
(значения ρ в таблице)

Сила жидкостей и газов

Сила давления на дно сосуда:

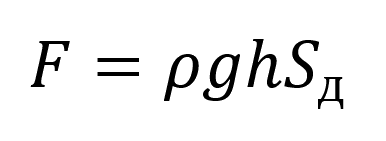
Пояснение:

F - приложенная сила (н)
ρ(ро) - плотность жидкости (кг/м³)
g - ускорение свободного падения (9,8 м/с²)
h - высота столба жидкости (м)
Sд - площадь дна сосуда (м²)
(значения ρ в таблице)

Сила давления на стенки сосуда:

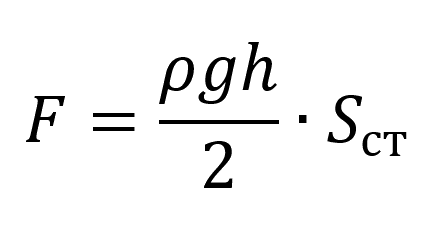
Пояснение:

F - приложенная сила (н)
ρ(ро) - плотность жидкости (кг/м³)
h - высота столба жидкости (м)
g - ускорение свободного падения (9,8 м/с²)
Sст - площадь стенок сосуда (м²)
(значения ρ в таблице)

Соотношение сил в гидравлическом прессе:

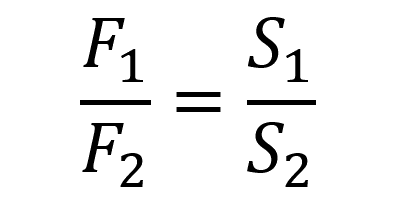
Пояснение:

F1 - сила, действующая на первый (обычно больший) поршень (н)
S1 - площадь первого поршня (м²)
F2 - сила, приложенная ко второму (обычно меньшему) поршню (н)
S2 - площадь второго поршня (м²)

Закон Архимеда, если тело плавает:

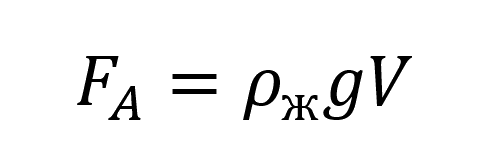
Пояснение:

FA - сила Архимеда (н)
ρ(ро) - плотность жидкости (кг/м³)
g - ускорение свободного падения (9,8 м/с²)
V - объём тела (м³)
(значения ρ в таблице)

Закон Архимеда, если тело полностью погруженно:

FA = mg

Пояснение:

FA - сила Архимеда (н)
m - масса тела (кг)
g - ускорение свободного падения (9,8 м/с²)